|
Mechanical System Modeling
The
equations of motion involving a rotary flexible link, involves
modeling the rotational base and the flexible link as rigid
bodies. As a simplification to the partial differential equation
describing the motion of a flexible link, a lumped single degree
of freedom approximation is used. We first start the derivation
of the dynamic model by computing various rotational moment
of inertia terms. The rotational inertia for a flexible link
and a light source attachment is given respectively by
|
|
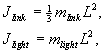
|
(1)
(2)
|
where
mlink is the total mass of the flexible link,
mlight is the mass of the light source compartment,
and L is the total flexible link length. Combining the
moment of inertia�s for both the link and the light source gives
|
|
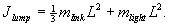
|
(3)
|
For
a single degree of freedom system, the natural frequency is
related with torsional stiffness and rotational inertia in the
following manner
|
|
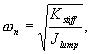
|
(4)
|
where
w n is found experimentally
and Kstiff is an equivalent torsion spring
constant as delineated through the following figure

In
addition, any frictional damping effects between the rotary
base and the flexible link are assumed negligible. Next, we
derive the generalized dynamic equation for the tip and base
dynamics using Lagrange�s energy equations in terms of a set
of generalized variables a and q,
where a is the angle of tip deflection
and q is the base rotation given
in the following
|
|
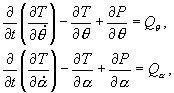
|
(5)
(6)
|
where
T is the total kinetic energy of the system, P is
the total potential energy of the system, and Qi is
the ith generalized force within the ith
degree of freedom. Kinetic energy of the the base and the flexible
link are given respectively as
|
|

|
(7)
(8)
|
The total kinetic energy of the mechanical system
is computed as the sum of (7) and (8)
|
|
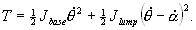
|
(9)
|
Potential energy of the system provided by the
torsional spring given as
|
|
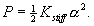
|
(10)
|
Applying equation (9) and (10) into (5) and
(6) results in the following dynamic equations
|
|
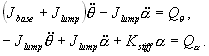
|
(11)
(12)
|
Next
we compute the amount of virtual work, W, applied into
the system. The amount of virtual work is given to be
|
|
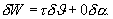
|
(13)
|
where t is
the torque applied to the rotational base. Rewriting equation
(13) into a general form of virtual work given as
|
|
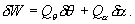
|
(14)
|
We
obtain the virtual forces applied onto the generalized coordinatesQq
and Qa , respectively
to be
|
|
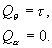
|
(15)
(16)
|
After
decoupling the acceleration terms of (11) and (12), the dynamic
equations for the mechanical subsystem are
|
|
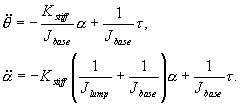
|
(17)
(18)
|
Next, rewriting equations (17) and (18) into
a state space form gives
|
|
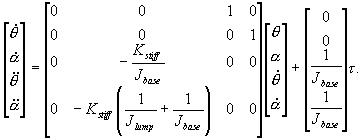
|
(19)
|
Electrical System Modeling
Since
the control input into the mechanical model of equation (19)
is a torque t , an electrical dynamic
equation relating voltage to torque is needed. First, the torque
applied to the rotational base, on the right hand side of equation
(19), is converted to the torque applied to the gear train by
the DC servomotor by means of a gear ratio Kg
given as
|
|
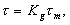
|
(20)
|
where
t m is the torque
applied by the servomotor. Next, the circuitry within the DC
motor system consists of a resistor, an inductor, an external
voltage source, and a back emf placed in a series circuit. The
following figure describes the circuit as previously described
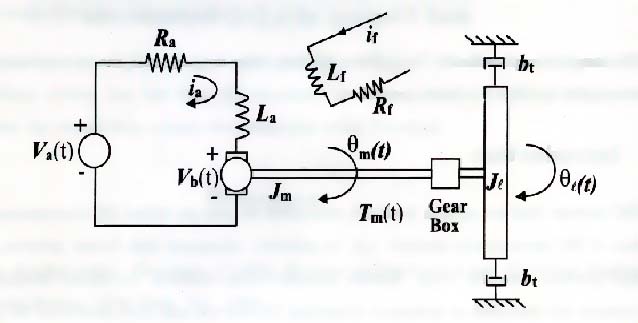
Applying
Kirchoff�s voltage law to the above figure, produces
|
|
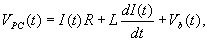
|
(21)
|
where I is the current in the circuit,
R is the resistor, L is the inductor, Vb
is the back emf, and VPC is the voltage supplied
by the data acquisition board. The DC servomotor is an electromechanical
device that relates torque to current through a proportionality
gain KT given in the following equation
|
|

|
(22)
|
In
addition, the back emf is a voltage applied by the motor shaft
to the circuit, which is directly proportional to the angular
velocity of the motor
|
|
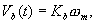
|
(23)
|
where
Kb is the back emf constant and w
m is the angular velocity of the motor. Relating
the motor angular velocity with the base angular velocity gives
|
|
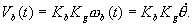
|
(24)
|
Substituting equations (22) and (24) into (21)
gives
|
|
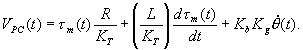
|
(25)
|
Since
the effect of the inductance in the circuit is relatively small
in comparison with other circuit components, the derivative
term of torque can be neglected eliminated to give the following
approximate proportionality equation between voltage to torque
and angular velocity
|
|
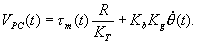
|
(26)
|
The torque applied by the motor is solved for
in equation (26) to be
|
|
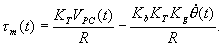
|
(27)
|
As
a result, the state space model of (19) can be rewritten to
utilize an electrical control voltage in (20) and (27) to give
|
|
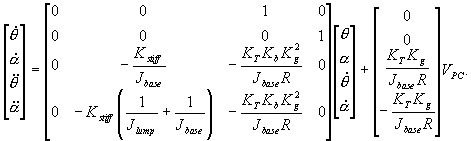
|
(28)
|
Next,
a transformation between relative angular position and relative
displacement about a neutral axis is used within the state space
model of (28). The relative angular position, velocity with
respect to the rotating base is proportional to the relative
displacement, velocity of the flexible link tip (i.e. sin(a)�a)
|
|
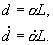
|
(29)
(30)
|
The following figure shows the relationship
of these three parameters.
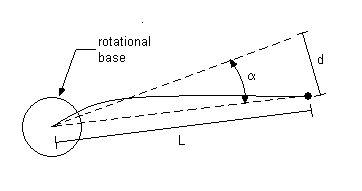
Substituting
the above equations of (29) and (30) into the state space dynamics
of (28) gives the following state space equation
|
|
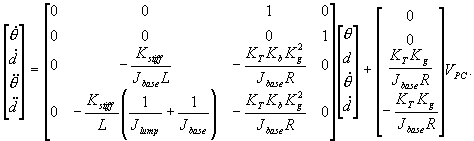
|
(31)
|
Control Objective
The
objective for the rotary flexible link dynamic system is to
achieve an asymptotically stable system response for flexible
link. A Linear Quadratic Regulator (LQR) based controller achieves
asymptotic stable response for a controllable state space model.
For the state variable of d(t), an LQR controller drives
the flexible dynamic response to zero asymptotically. However,
for the angular position tracking of 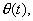 a
new state variable is required to allow for setpoint tracking.
To achieve error regulation for a
new state variable is required to allow for setpoint tracking.
To achieve error regulation for 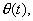 an angular displacement error and an angular velocity error
term is defined respectively as
an angular displacement error and an angular velocity error
term is defined respectively as
|
|

|
(32)
(33)
|
where
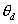 is a desired constant angular position for the flexible link.
In addition, an integral controller coupled in the rigid body
dynamics is defined within the state space dynamics of (31)
is a desired constant angular position for the flexible link.
In addition, an integral controller coupled in the rigid body
dynamics is defined within the state space dynamics of (31)
|
|
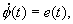
|
(34)
|
so that the state space dynamics of (31) is
augmented with (34) to give the following model
|
|
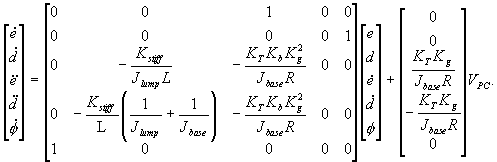
|
(35)
|
As
a result, the continuous time state space equation of (35) is
converted numerically into a discrete time state space equation
using Matlab. The resulting discrete time dynamic model is
|
|

|
(36)
|
Controller Design
Given
a 5th order system given in equation (36), the control
objective involves error regulation for the absolute angular
displacement of the rotary base and vibration control for the
end of the flexible link. A full state feedback control law
given by
|
|
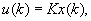
|
(37)
|
where K Î
 1�
5 such that the full state feedback control law of (37)
satisfies the following criteria
-
The closed loop state space system is
asymptotically stable
-
The performance functional given by
|
|

|
(38)
|
where
 are
the state vectors and control inputs, respectively. The performance
functional of equation (38) regulates the state trajectories
of x(k) close to the origin without excessive control
demand through the design of the penalty weights of Q and
R. The nonnegative definite matrix Q Î
 5�
5, determines the weight placed on each component of state.
The nonnegative definite matrix R Î
 1 determines
the weight placed on the control input. The state feedback control
law given in (37) is computed through the following matrix equation are
the state vectors and control inputs, respectively. The performance
functional of equation (38) regulates the state trajectories
of x(k) close to the origin without excessive control
demand through the design of the penalty weights of Q and
R. The nonnegative definite matrix Q Î
 5�
5, determines the weight placed on each component of state.
The nonnegative definite matrix R Î
 1 determines
the weight placed on the control input. The state feedback control
law given in (37) is computed through the following matrix equation
|
|
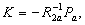
|
(39)
|
where R2a and Pa
are defined as
|
|
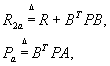
|
(40)
|
such that the nonnegative definite matrix P
solves the following Ricatti equation
|
|
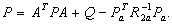
|
(41)
|
The computation of equation (37) is performed
numerically using Matlab resulting in the following set of state
feedback control gains:
|
|
Control Gains
|
|
|
K1 (V/deg)
|
K2 (V/cm)
|
K3 (V/deg)
|
K4 (V/cm)
|
K5 (V/deg)
|
|
0.2874
|
-0.8115
|
0.0516
|
-0.0017
|
0.1169
|
Experimental Setup
Matlab Controller Design
To
implement the Linear Quadratic Regulator, various system parameters
need to be defined. The following m-file provides all known
system parameters for use in Matlab: Parameters.m
In
addition, the state space matrix equation of (35) is defined
to compute the LQR gains for block diagram implementation. Two
first order noise and derivative filters are designed by specifying
a cutoff frequency. The m-file involves designing the filters
first in the continuous domain using Laplace transfer functions
and converting the continuous filters to the discrete domain.
The following m-files compute the state space model in addition
with the state feedback controller gains and digital filters
used in the experiment:
Model.m
Controller.m
The
implementation of the state feedback controller is performed
using a Simulink block diagram instead of manual C code generation.
Consequently, Simulink controller design compiles the block
diagrams into C code for hardware use. The following figure
shows the Simulink block diagram for the flexible link full
state feedback controller:
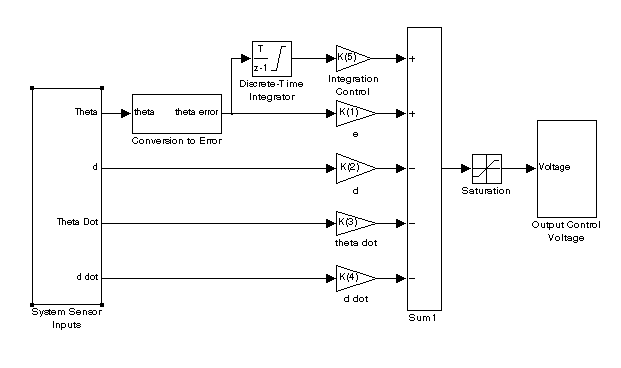
The
summing block in the previous figure gives the full voltage
control input into the rotary flexible link motor to be converted
into torque. The saturation block in the above figure is added
to prevent voltage overflow into the data acquisition board
(only capable of inputting and outputting �
5 volts). Also, the following Simulink block diagram defines
the subsystem of "System Sensor Inputs":
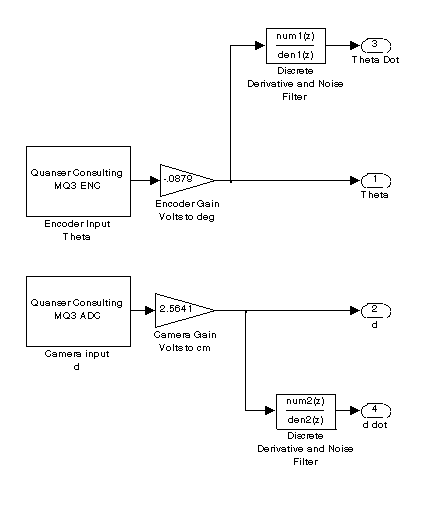
The
discrete derivative and noise filters for the encoder and camera
inputs are utilized through a continuous transfer function design
for a specified cutoff frequency integrated into a discrete
time transfer function model. An encoder calibration is utilized
to converted voltage to degrees from the encoder signal. The
camera input is converted from voltage to centimeters through
an experimental calibration gain. The "Output Control Voltage"
subsystem is given to be:
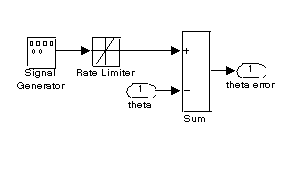
The "Conversion to Error" subsystem is defined
as:
|